MS/MS
Fragmentation in the Drift Tube
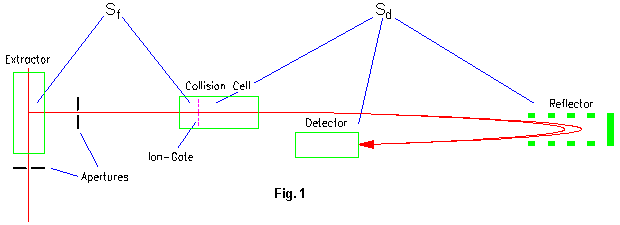
The usual mode of operation for a Time-of-Flight mass spectrometer is to take a packet of ions in the ion optics and pass this packet unhindered and unmodified to the detector. Looking at Fig. 1 this would mean the ion gate is open and there is no gas in the collision cell. This way we will get a mass spectrum showing the masses of the intact ions.
In order to get structural information about the (molecular) ions just measured, we have to break them up and measure the weights of the fragments. This is done by filling the collision cell with a gas, preferably Helium. The ions will then collide with the Helium atoms, these collisions exiting internal vibrations. When the amplitude of the vibrations becomes too high the ions will start breaking apart, usually tearing up the weakest bonds first. These weakest bonds are in most cases the links between subgroups of the molecules.
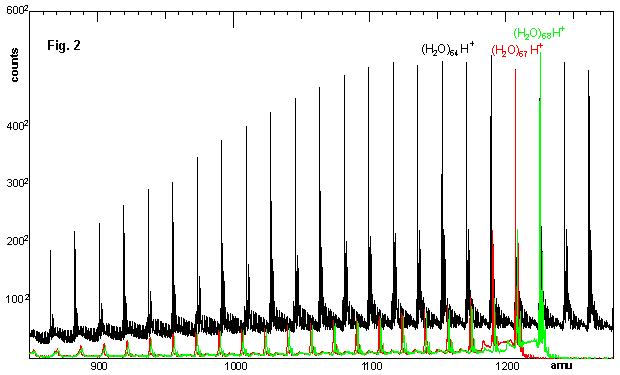
Lets first look at the experimental results of fragmenting molecules in the drift tube, and then attempt to put this into mathematical formulas. Fig. 2 shows three mass spectra of water clusters:
The black trace shows water clusters going through the collision cell filled with Helium, the ion gate wide open, i.e. letting molecules of all masses pass through.
The red trace shows again the water clusters going through the collision cell, but the ion gate is only open when the (H2O)67H+ cluster passes through it. Thus the water clusters of smaller mass showing up in the mass spectrum must be fragments from the original (H2O)67H+ cluster.
The green trace is like the red trace, except the ion gate opens only for the (H2O)68H+ cluster.
Two things are immediately apparent from Fig. 2:
The black trace shows a lot of ‘junk’ around the baseline. However, looking more carefully we will find out that this junk is not just increased background, but all comes from fragmentation of larger clusters. This means there is actually a lot of information in this spectrum.
Looking more closely at the red and green trace, we see where this ‘junk’ comes from: Each small peak between two large cluster peaks is the fragment of one specific larger cluster peak. Thus the position of a fragment peak already gives an information about the size of the fragment it has lost or the position of its parent peak.
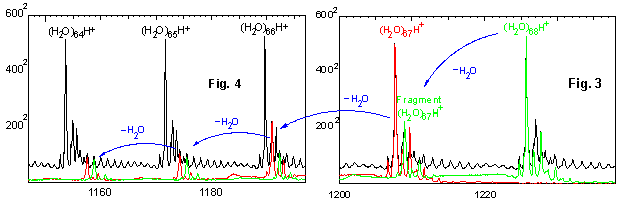
Fig. 3 shows the (H2O)67H+ and the (H2O)68H+ cluster and mingled in between the isotopes of the (H2O)67H+ cluster the first fragment of the (H2O)68H+ cluster, i.e. a (H2O)68H+ cluster having lost one water molecule. Very well it can be seen where the isotopes of the first fragment are and how different fragments will add up to the resulting spectrum which is the black trace.
Stepping some 17 or 18 mass units to lower mass, we can see in Fig. 4 around mass 1190 the first fragment of the (H2O)67H+ cluster and the second fragment of the (H2O)68H+ cluster. A little bit further to the left we then find the second fragment of the (H2O)67H+ cluster and the third fragment of the (H2O)68H+ cluster. Fig. 2 shows how this series continues over many fragment losses.
Thus the most important piece of information we gather from the figures above is that if a molecule looses some part of its constituents, it will not appear exactly at the mass of its residual mass but at a mass somewhat higher. Actually this shift towards higher mass is proportional to the mass of the fragment that has been lost in the drift tube, this factor of proportionality being a calibration constant specific to each instrument.
Looking again to Fig. 1 this fragment shift can easily be understood. Just divide the path of an ion between the extractor and the detector into two segments:
the path from the extractor up to the ion gate (within the collision cell). Call the length of time the ion needs for this segment Sf.
the path from the ion gate to the detector. Call the length of time the ions needs for this segment Sd.
Call the length of time the ion needs for the complete path S.
The idea of separating the path into these two segments is that the point of separation is a time focus point, i.e. a point in space which all ions of the same mass simultaneously pass, irrespective of their initial kinetic or potential energy. This time focus point is called Wiley-McLaren focus, and the time an ions needs on any one of the segments is only a function of its mass and not of its initial or final energy. (Note that an ion loosing some mass on its flight also looses some energy, which would very much complicate our calculation if we did not split up the path in the above way.)
Now all you have to do is compare two paths of two particles:
Of a particle of residual mass that has started with this mass right from the extractor, has gone unhindered through the collision cell on to the detector.
Of a particle that has started with the parent mass, has lost the fragment mass in the collision cell, thus continuing after the collision cell with the residual mass.
On the second segment this particle needs the same time as the unfragmented particle.
On the first segment this particle will need a somewhat longer time due to its larger mass there. Actually on this segment the time-of-flight will depend very simply on the square root of the mass the particle has there.
Since the first segment is only a part of the complete path, this means that if the particle had a higher mass on this segment, the mass or time shift incurred on this segment must be multiplied ratio of the first time segment divided by the complete time-of-flight, thus
m + dm = m + mf*Sf/S
where
m : is the final mass of the particle
dm : is the apparent mass shift of the residual particle after fragmentation
mf : is the mass of the fragment lost in the collision cell
Sf/S : is the ratio of the length of the first segment to the total length of the flight path